第十三章:Validium 代表项目 StarkEx
这里不再做过多的叙述,请看文档, StarkEx 中文文档: https://docs.starkware.co/starkex-docs-v2-chinese/
下面简单说一下文档中提到的 merkle 树 和 稀疏默克尔树
如果你最近去过以太坊研究社区,你可能听说过一种叫做稀疏默克尔树的东西。它们可能听起来很吓人,但它们真的很简单。这篇文章将准确解释什么是稀疏 Merkle 树,为什么它们很酷,以及它们目前的用途。
一. 默克尔树
首先,让我们先快速复习一下 Merkle 树。Merkle 树为我们提供了一种以加密方式提交一组数据的方法。我们首先对集合中的每条数据进行散列,然后继续沿着树向上散列,直到到达根节点。
最终看起来像这样:
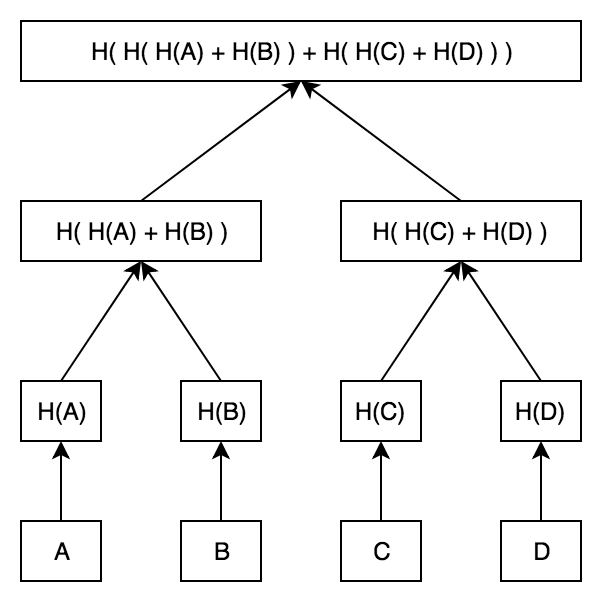
1.证明包容
这棵树的根只是一个散列——它没有告诉我们树的内容。我们可以使用一种叫做“Merkle proof”的东西来证明某些内容实际上是这棵树的一部分。例如,让我们证明它A是上述树的一部分。我们需要做的就是A在向上的过程中提供每个兄弟姐妹,重新计算树,并确保一切都匹配。
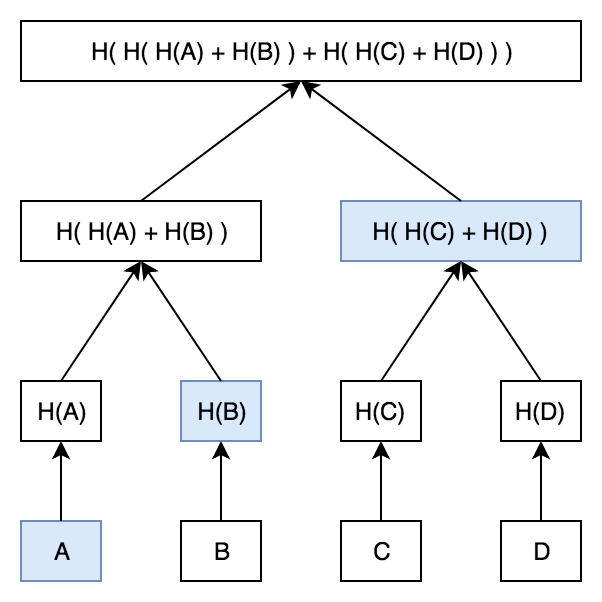
我继续用蓝色突出显示兄弟姐妹。只需A、H(B)和H(H(C)+H(D)),我们就可以重新计算原始根哈希。这是一种有效的方式来显示它A是这棵树的一部分,而无需提供整个树!
1.证明不包含
所以我们可以很容易地证明某物是默克尔树的一部分,但是如果我们想证明某物不是默克尔树的一部分呢?不幸的是,标准的默克尔树并没有给我们任何好的方法来做到这一点。我们可以透露全部内容,但这有点违背了首先使用 Merkle 树的意义。
二.稀疏默克尔树
这就是稀疏默克尔树发挥作用的地方。稀疏 Merkle 树类似于标准 Merkle 树,不同之处在于包含的数据被索引,并且每个数据点都放置在与该数据点的索引对应的叶子上。
假设我们有一棵有四片叶子的 Merkle 树。我们将用一些字母 ( A, D) 填充这棵树以进行演示。字母A是字母表的第一个字母,所以我们应该把它放在第一页。同样,我们可以放在D第四片叶子上。
那么第二片和第三片叶子会发生什么?我们只是让它们空着。更准确地说,我们放置一个特殊值(如null)而不是放置一个字母。
树最终看起来像这样:
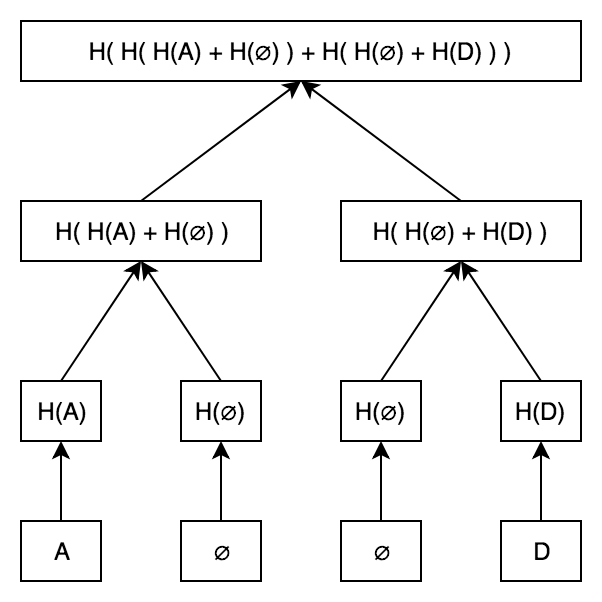
1. 证明包容
就像在标准的 Merkle 树中一样,我们可以使用 Merkle 证明来证明它A是这棵树的一部分。这个证明看起来就像你的标准 Merkle 证明:
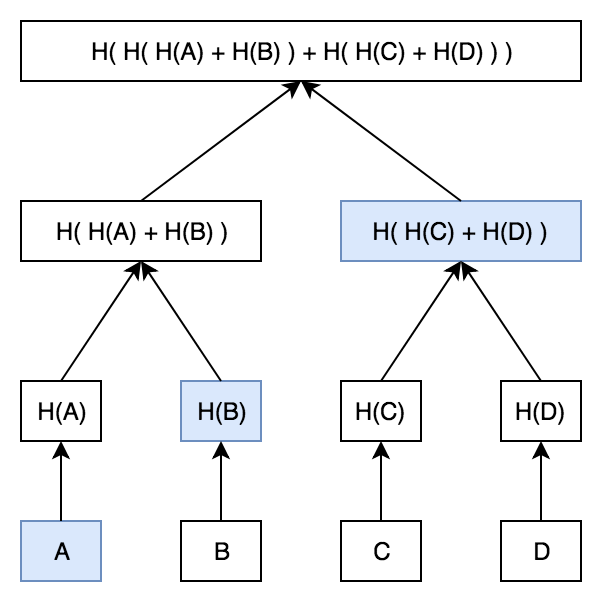
同样,我们只是提供兄弟姐妹H(null)和H(H(null)+H(D)),并检查它是否与根匹配。
2. 证明不包含
这就是魔法发生的地方。如果我们想证明它C不是这棵Merkle 树的一部分,会发生什么?这简单!我们知道,如果C是树的一部分,它会在第三片叶子上。如果C不是 树的一部分,则第三片叶子必须是null。
我们所需要的只是一个标准的默克尔证明,显示第三片叶子是null!
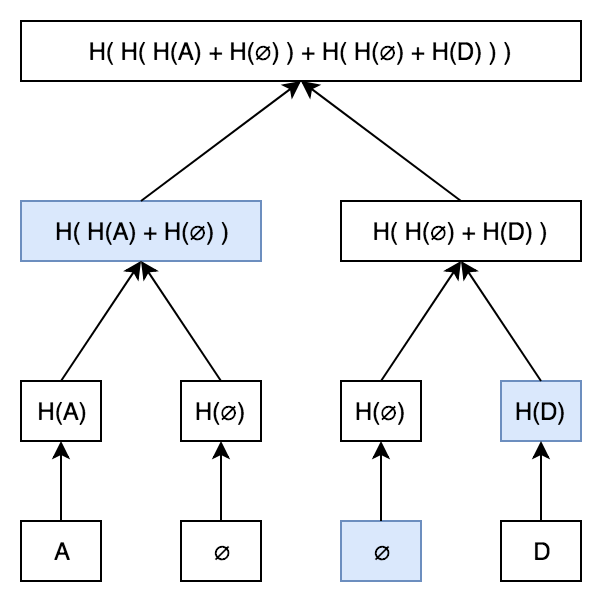
这看起来就像一个标准的 Merkle 证明,除了我们证明叶子包含null而不是C.
稀疏 Merkle 树的最佳部分是它们真正代表了 Merkle 树内部的键值存储!
3. 缺点
稀疏默克尔树真的很酷,因为它们为我们提供了不包含的有效证明。然而,这也可能意味着它们变得非常非常大。26 个字母并不多,但大多数时候我们谈论的是 2²⁵⁶ 哈希!手动生成树的索引太多了。
幸运的是,有一些技术可以有效地生成 Merkle 树。这些技术的关键在于,这些巨大的稀疏 Merkle 树大多是……稀疏的。H(null)是一个常数值,H(H(null))等等等等。树的大块可以被缓存!
4. 用例
稀疏默克尔树已经在野外被用来做一些很酷的区块链事情。
Plasma Cash利用稀疏的默克尔树来存储有关存入资产的信息。每个 Plasma Cash 资产都有一个唯一的 ID。每当资产转移给新用户时,交易都会包含在资产索引处的稀疏 Merkle 树中!包含证明(或不包含!)用于证明给定的交易历史是有效的。
稀疏的默克尔树甚至可能进入以太坊!以太坊研究人员正在研究稀疏的 Merkle 树,以替代目前用于存储以太坊状态的 Merkle Patricia 尝试。
